Fonction trigonométriques utilisées en physique (Ondes notamment)
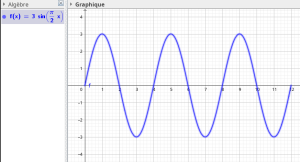
Exemple : Avec un sinus
\(f(t)=3 sin \left( \frac{\pi}{2} t \right)\)
L'amplitude est \(A=3\)
La période est \(T=.4.\) (donc la fréquence est \(f= \frac{1}{T} = \frac{1}{4}\))
La phase à l'origine est \(\phi=0\)
Exemple : Avec un cosinus
\(g(t)=3 ~cos \left( \pi t + \frac{\pi}{2} \right)\)
L'amplitude est \(A=3\)
La période est \(T=2\) (donc la fréquence est \(f= \frac{1}{2}\))
La phase à l'origine est \(\phi=\frac{\pi}{2}\)
Méthode : Amplitude, période, phase d'un signal sinusoïdal
Si \(f\) est une fonction de la forme \(A sin(\omega t + \phi)\) ou encore \(A cos(\omega t + \phi)\),
Alors :
L'amplitude est \(A\).
La période est \(\boxed {T=\frac{2\pi}{\omega}}\) (et la fréquence est \(f=\frac{1}{T}\))
La phase à l'origine est \(\phi\).
La phase instantanée est \(\omega t + \phi)\).