Les 1ères suites
Définition : Qu'est ce qu'une suite ?
Une suite numérique est une liste infinie et numérotée de nombres réels.
Fondamental :
Chaque terme de la suite se note \(u_n\) où \(n\) est le numéro du terme dans la liste.
La suite (c'est à dire l'infinité de ses termes) se note \((u_n)\).
\(u_{n+1}\) est le terme suivant le terme \(u_n\).
\(u_{n-1}\) est le terme précédant \(u_n\).
\(u_n\) et \(u_{n+1}\) sont des termes consécutifs.
Exemple :
Suite définie par une relation de récurrence :
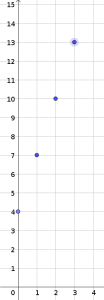
\(4\ \ 7\ \ 10 \ \ 13\ \ ...\) est la suite numérique de 1er terme 4 pour laquelle on passe d'un terme au terme suivant en ajoutant toujours 3.
Elle correspond au tableau de valeurs :
\(n\) | 0 | 1 | 2 | 3 | ... |
\(u_n\) | 4 | 7 | 10 | 13 | ... |
Afin de connaître cette suite, on écrit : \(u_0=0\) et, pour tout entier naturel \(n\), \(u_{n+1}=u_n+3\)
Représentation graphique :
Exemple :
Suite définie de façon explicite :
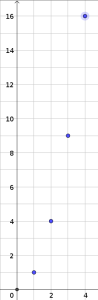
\(0\ \ 1\ \ 4 \ \ 9\ \ 16\ \ ...\) est la suite des carrés des entiers naturels ("carrés parfaits").
Elle correspond au tableau de valeurs :
\(n\) | 0 | 1 | 2 | 3 | 4 | ... |
\(u_n\) | 0 | 1 | 4 | 9 | 16 | ... |
Afin de connaître cette suite, on écrit :
pour tout entier naturel \(n\), \(u_n=n^2\).
Représentation graphique :
